Leibniz

3.1.2 Productividad marginal decreciente

La función de producción de Alexei tiene la propiedad de productividad marginal decreciente. Podemos verlo gráficamente: el gráfico se hace más plano a medida que aumentan las horas de estudio por día. ¿Qué significa esto para las propiedades matemáticas de la función de producción?

Si la función de producción es $y=f(h)$, entonces la productividad marginal del trabajo es $\frac{dy}{dh}=f’(h)$, así que el producto marginal del trabajo disminuye a medida que $h$ aumenta si:

$$\frac{d}{dh}\left( \frac{dy}{dh} \right) = \frac{d^{2}y}{dh^{2}} < 0$$

O lo que es lo mismo:

$$f’’(h) \lt 0$$

Es decir, si la segunda derivada de la función de producción es negativa.

Un ejemplo

Considere nuevamente la función de producción:

$$y = Ah^\alpha$$

dónde $A$ y $\alpha$ son constantes tales que $A \gt 0$ y $0 \lt \alpha \lt 1$. En el Leibniz 3.1.1 mostramos que, para esta función de producción,

$$\text{PMT} = \frac{dy}{dh} = \alpha Ah^{\alpha -1}$$

que es positiva siempre y cuando las horas de estudio $h$ sean positivas. Lo que queremos mostrar a continuación es que, al aumentar las horas $h$, este producto marginal se hace cada vez más pequeño.

Una forma de verlo es centrarse en la expresión

$$\alpha Ah^{\alpha -1}$$

donde se eleva $h$ a la potencia $\alpha -1$, que es negativa porque $\alpha \lt 1$. Recordemos que, según las propiedades de la exponenciación a exponentes negativos, cuando $h$ aumenta, $h^{\alpha -1}$ disminuye y, como tanto $A$ como $\alpha$ son positivos, entonces la expresión $\alpha Ah^{\alpha -1}$ –la productividad marginal del trabajo–, también disminuye.

De manera alternativa, podemos mostrar que el producto marginal está disminuyendo si derivamos:

$$\frac{d^2 y}{dh^2} = (\alpha -1)\alpha Ah^{\alpha -2}= \alpha(\alpha -1)\frac{Ah^\alpha}{h^2} =\alpha(\alpha -1)\frac{y}{h^2}$$

Cuando $h$ es positivo, sabemos que $y$ es positivo también. Entonces cuando $0 \lt \alpha \lt 1$, $\alpha(\alpha -1) \lt 0$, por lo que:

$$\frac{d^2 y}{dh^2} =\alpha(\alpha -1)\frac{y}{h^2} \lt 0$$

que es lo que se quiere demostrar: la segunda derivada de la función de producción es negativa, por lo que el producto marginal cae cuando $h$ aumenta. En otras palabras, el producto marginal del trabajo es decreciente.

En el Leibniz 3.1.1 mostramos que, cuando $\alpha \lt 1$, el producto marginal es menor que el producto promedio. Esta propiedad está estrechamente relacionada con el concepto de productividad marginal decreciente: si el producto marginal de una función de producción es decreciente para todos los valores de la variable independiente (el insumo), también es cierto que el producto marginal es menor que el producto promedio (PMT < PMeT).

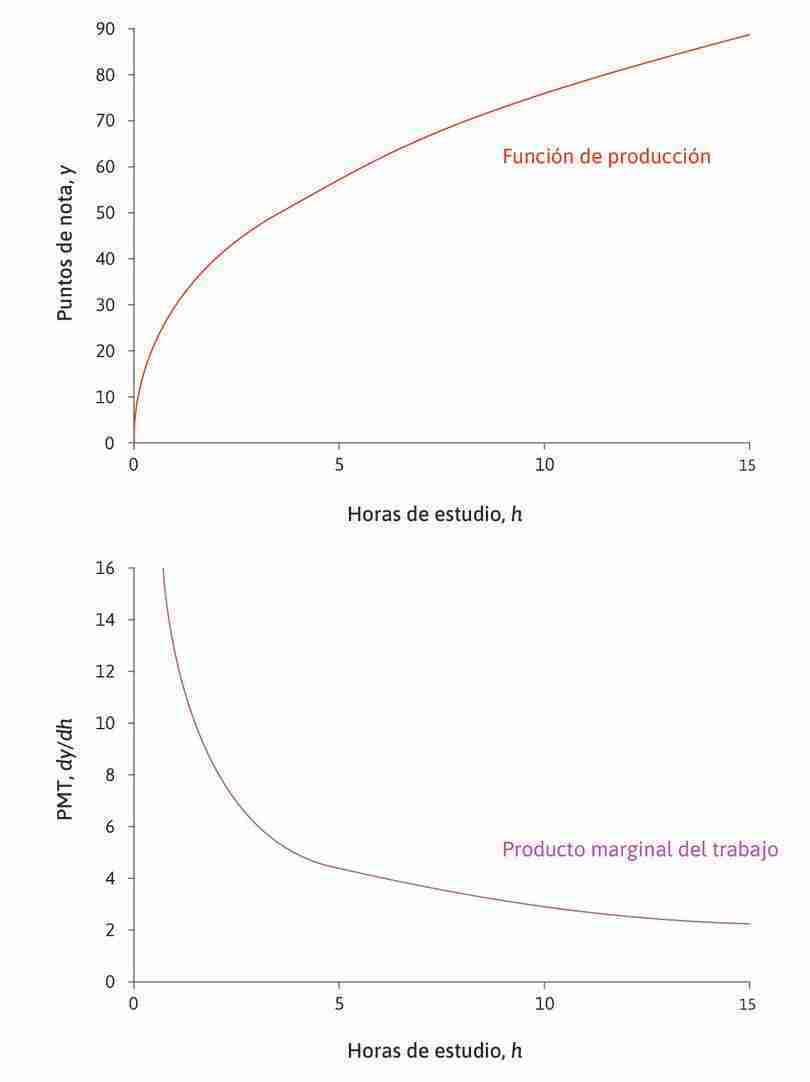
La figura 2 muestra la gráfica de la función de producción $y = Ah^\alpha$ para el caso en que $\alpha =0,4$ y $A=30$, junto con la gráfica del producto marginal del trabajo. Para cada valor de $h$, el gráfico superior muestra el valor de $y$ y el gráfico inferior muestra la pendiente de la función de producción, $dy/dh$. Se puede ver que el producto marginal del trabajo disminuye con (el aumento de) $h$.

Puede leer más sobre este tema en las secciones 6.4 y 8.4 de Pemberton y Rau (2016).